Lattice path associated to a numerical semigroup
Definition
Let \(S\) be a numerical semigroup, let \(p,q\) be two coprime in \(S\) and \(H_{p,q} = \langle p, q \rangle\). It holds that \(H_{p,q}\) is a numerical semigroup and \(H_{p,q} \subseteq S\), then every gap of \(S\) is a gap of \(H_{p,q}\). If \(c\) is the conductor of \(H_{p,q}\), every gap \(g\) of \(H_{p,q}\) can be written uniquely as \(g = c - 1 - (ap + bq)\), for some non-negative integers \(a,b\). It is said that \((a,b)\) are the coordinates associated to \(g\). Let \(H(a,b)\) be the set of coordinates of the gaps of \(H_{p,q}\). Then, it is defined the lattice path of \(S\) with respect to \(H_{p,q}\), denoted by \(P_{p,q}\), as the path in \(\mathbb{N}^2\),
\[ P_{p,q} = \{(a_1, b_1), \ldots, (a_n, b_n) \} \subseteq H(a,b), \]
such that every element in \(H(a,b)\) is below the lattice path.
From the definition, there is no gap in the line \(px + qy = c-1\) and every point \((a,b) \in \mathbb{N}^2\) below the line is an element of \(H(a,b)\).
Examples
\(\circ\) Let \(S = \langle 5, 7, 9, 11, 13 \rangle = \{0, 5, 7, 9, \rightarrow\}\) and \(p = 5, q = 7\). The set of gaps of \(S\) is \(G(S) = \{1, 2, 3, 4, 6, 8\}\). On the other hand, \(H_{p,q} = \langle 5, 7 \rangle\) has conductor \(C(H_{p,q})-1 = pq - p - q -1 = 23\), then \(P = C(H_{p,q}) - 1 - G(S) = \{22, 21, 20, 19, 17, 15\}\) and its coordinates are \(P' = \{(3,1), (0,3), (4,0), (1,2), (2,1), (3,0)\}\) ordered as in \(P\). Considering the line \(5x + 7y = 23\), we have the following situation.
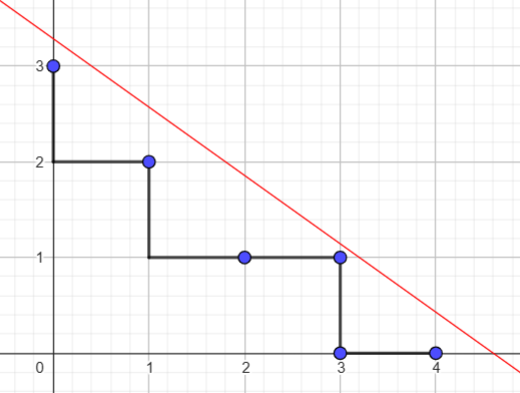
The red line is the line \(5x + 7y = 23\) and the blue points are the coordinates of the gaps of \(S\). As we can see in the image, the lattice path of \(S\) with respect to \(H_{5,7}\) is \(P = \{(0,3), (1,2), (3,1), (4,0)\}\).
Examples with GAP
The following example is made with the package NumericalSgps in GAP.
\(\diamond\) Let \(S = \langle 16,17,71,72 \rangle\), in GAP:
gap> S := NumericalSemigroup(16,17,71,72);
<Numerical semigroup with 4 generators>Given a numerical semigroup \(S\) and two integers \(p,q\) such that \(\gcd (p,q) = 1\), the function LatticePathAssociatedToNumericalSemigroup returns the lattice path of \(S\) with respect to \(H_{p,q}\).
gap> LatticePathAssociatedToNumericalSemigroup(S, 16, 17);
[ [ 0, 14 ], [ 1, 13 ], [ 2, 12 ], [ 3, 11 ], [ 4, 10 ], [ 5, 9 ], [ 6, 8 ],
[ 7, 7 ], [ 8, 6 ], [ 9, 5 ], [ 10, 4 ], [ 11, 3 ], [ 12, 2 ], [ 13, 1 ],
[ 14, 0 ] ]The result is as follows.
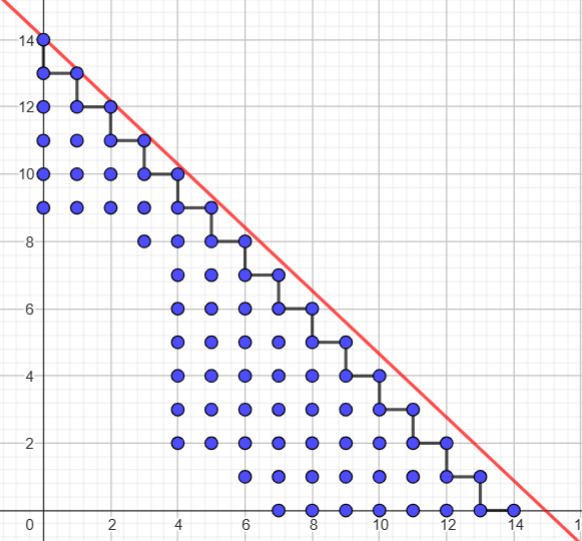
As before, the red line denotes the line \(ax + by = c-1\) and the blue points are the coordinates of the gaps of \(S\).
References
https://gap-packages.github.io/ numericalsgps.